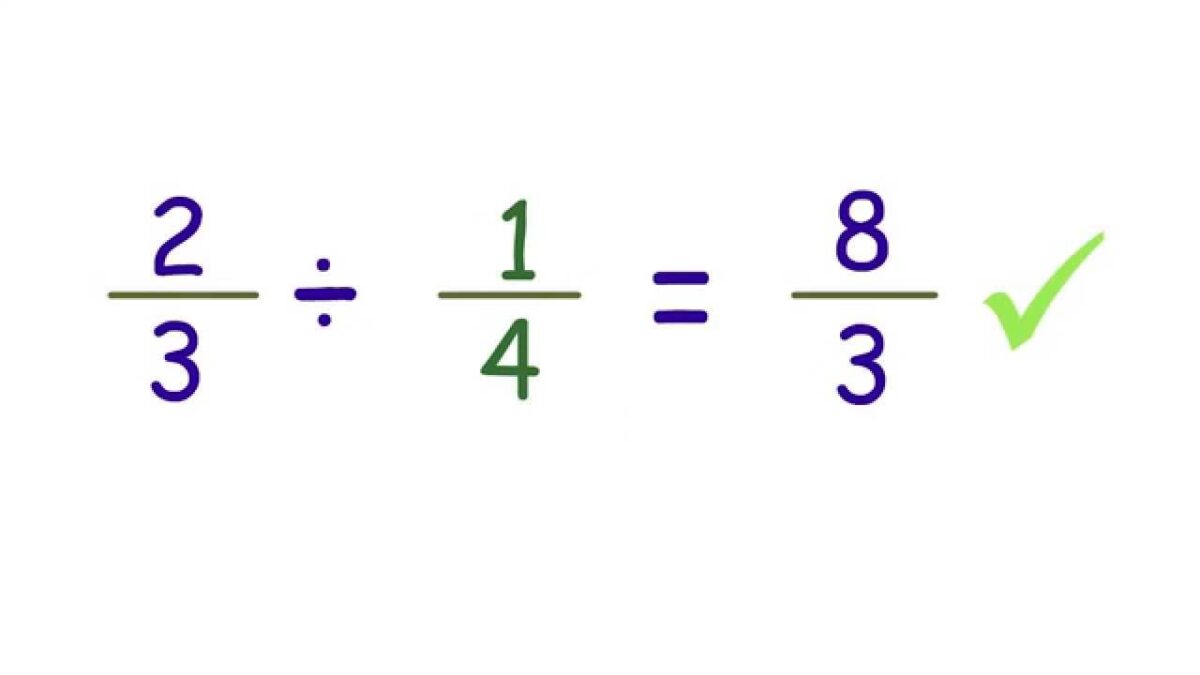If you are confused about fractions division then the guide here will clear all the doubts related to it. It is easy to get the right answer once you learn all the little tricks. Nevertheless, when teaching division, you do not want your students merely to solve problems. The purpose of each question is to help the student understand what the basics are and go into depth. The division of fractions is not simple, thus, the guide explains how you can make sure you master the key concepts required to divide fractions. In this article, you will learn to master fraction division. Pay attention, and you will be a fraction division expert in no time.
How to divide fractions?
It is important to notice what the answer means when you divide the fractions. Here is an example:
½ ÷ ⅙ = 3
Can you explain why the answer is greater than the fractions? By dividing a fraction, you are asking how many groups of the divisor which is the second number are in the dividend, which is the first number. With the equation above, we want to know how many of the ⅙ appear in ½.
As an example, think of an equation as a cake. You still have half of the cake left. What is the remaining number of servings of cake if each serving is ⅙ of the whole? Three pieces of cake are left, as you can see!
Hope you are clear with the concepts of the division of fractions. Remember the key rules for fraction division which is to flip the fractions and then multiplying fractions. You will master these types of questions in no time. You should practice more questions and enroll in platforms like cuemath.com to strengthen the concepts.
Let’s learn the methods to divide fractions
Dividing fractions the way you would divide a regular math problem would likely result in complex fractions. Thus, it would not be a good idea to go ahead. The good news is that the process of dividing fractions is much simpler if you use a shortcut. Following these three steps will help you solve most division problems:
- To reverse the divisor, flip it into a reciprocal
- Transform the division symbol into a “multiply” symbol to proceed with multiplication
- If possible, make your answer as simple as possible
This simplifies the process of dividing and helps you avoid complex fractions.
How to divide improper fractions?
Numerators with values that are greater than denominators constitute improper fractions. These fractions can be confusing, but the order of operations remains the same.
Even if the fraction is improper, the divisor is still flipped into a reciprocal, and the two fractions are multiplied.
How to divide mixed fractions?
If you have a fraction and a whole number, it’s called a mixed fraction. A mixed fraction, for example, would be 2 ½. What is the best way for the division of mixed fractions?
Follow the three-step strategy by making an improper fraction from the mixed fraction. Multiplying the denominator by the whole number will give you the answer. Adding this value to the numerator is the next step. For example, 2 ½ would become ⁵⁄₂.
Example 1:
3 ⅓ ÷ ⅖ =? → ¹⁰⁄₃ ÷ ⅖ =? → ¹⁰⁄₃ × ⁵⁄₂ = ⁵⁰⁄₆ → ²⁵⁄₃ → 8 ⅓
Example 2:
¼ ÷ 2 ⅙ =? → ¼ ÷ ¹³⁄₆ =? → ¼ × ⁶⁄₁₃ = ⁶⁄₅₂ → ³⁄₂₆
Example 3:
2 ½ ÷ 1 ⅓ =? → ⁵⁄₂ ÷ ⁴⁄₃=? → ⁵⁄₂ × ¾ = ¹⁵⁄₈ → 1 ⅞
How to divide fractions with whole numbers?
There is a similarity between problems involving whole numbers and mixed fractions. To divide an entire number, it must first be reduced to a fraction. Make the denominator one and the numerator the whole number when you want to turn a whole number into a fraction. For example:
3 → ³⁄₁
The three-step strategy can be used to solve the problem once the whole number is turned into a fraction. Example:
⅓ ÷ 3 =? → ⅓ ÷ ³⁄₁=? → ⅓ × ⅓ = ⅑
How to divide fractions with the same denominator?
It’s not necessary to find the reciprocal or multiply when you’ve got the same denominator. The answer can be obtained by dividing your fractions. Each denominator will cancel the other out and give you one. It is possible to simplify any fraction in which one is the denominator.
For example,
⅘ ÷ ⅖ = ²⁄₁ → 2